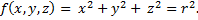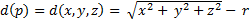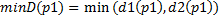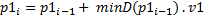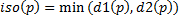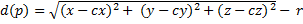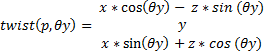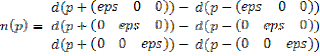Back from the #main 2009, while i looked at the BBS pouet, I came across the following thread: "So, what do remote field equations look like? And how do we solve them?" . Trivial question, but first answers didn't enlighten me about the basic understanding that i had already, but the main principle was still a bit obscure for me. But Ferris then posted a link to an article by John C. Hart, "Sphere tracing: a geometric method for the antialiased ray tracing of implicit surfaces" in 1996 and iq referred to two articles, a first even older John C. Hart, "Ray Tracing Deterministic 3-D Fractals" dating from 1989 and a resumption of the principle in the "Chapter 8. Per-Pixel Displacement Mapping with Distance Functions "of the book GPU from NVidia-Gems2 dating from 2004. Browsing the original article by John C. Hart, everything became clear! This article is an attempt to restore you some of the basic principle of RayMarching + DistanceFields, or more explicitly called Sphere Tracing.
The general principle
I will not detail the concept of raytracing, but I'll just put in relation with the RayMarching. To make a rendering, raytracing needs to calculate the intersection of the beam of vision with an object in the scene (to extract information from the surface material: diffuse color, refraction, diffraction, etc ....) And Therefore, to calculate formulas of intersections for each object. In the case where an object is modeled by a set of triangles, it requires to calculate the intersection of the ray with each triangle in the scene to determine which object is concerned by the beam. The calculation of intersections is very easy to implement, the formulas are established, so there is no problems, except for performance, since we must compute the intersection of the beam with a substantial number of surfaces (even if there are some way accelerate the division of space through eg K-d Trees).However, when one wants to represent implicit surfaces continuous or discontinuous (also called "Level surface" or "isosurface"), it is much more difficult to calculate this intersection since it would require the calculation of intersection between the equation of surface (Fig.1) and the path of a ray. This calculation would be specific to each equation. Thus, if the principle of a raytracing rendering is based on the intersection of the ray cast with objects in a scene, how to compute efficiently the intersection of the ray with an implicit surfaces?
Definition of an implicit surface. Fig.1 (see Wikipedia)
Before discussing the intersection RayMarching, we make a little reminder to inform our discussion. In the example given of a simple sphere of radius r (origin 0): the algebraic formula is :
Representing as distance, the sphere can be written differently:
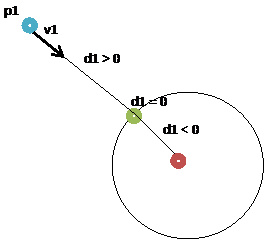
To calculate the intersection with sp1 a sphere of radius r1 using RayMarching with a radius of vision behind p1 (x1, y1, z1) and direction v1 (VX1, VY1, VZ1), we will from the origin of the radius (x1, y1, z1), calculate the distance to the surface of the sphere, by substituting the following:
And with the following properties for d1:
- If d1 = 0, then the point (x1, y1, z1) is located exactly on the surface of the sphere
- If d1 < 0, then the point (x1, y1, z1) is a distance | d1 | inside surface.
- If d1 > 0, then the point (x1, y1, z1) is a distance | d1 | outside surface.
If d1 > 0, the point p1 is outside the sphere, it suffices to calculate the intersection i1, we have to move from p1 to a distance of d1 in the direction of v1: i1 = p1 + d1v1
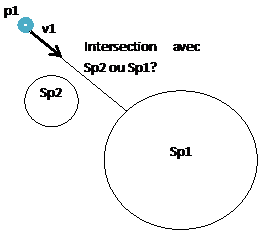
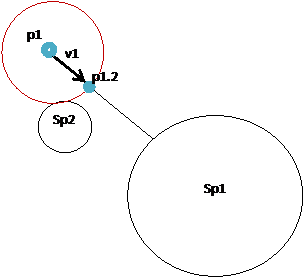
In the case of a single sphere, the calculation of intersection using the method of RayMarching is fairly trivial (and not really more interesting than analytical resolution), but if we have a more complex form, we can't determine the intersection at once. Take the example of a second sphere which would be added to the previous scene:
We want to determine on which sphere (p1, v1) intersects. With a single sphere, we have determined this intersection easily moving p1 to d1.v1. But with another sphere sp2, how can we move forward without colliding with sp2? If we move to d1 without checking, and it is found that sp2 is on the way, we'll skip sp2 and miss the intersection with sp2.
However, we know that the distance between p1 and sp2 is :
The trick is to move towards v1 to the minimum distance of all objects in the scene. So we move a step toward the intersection, a step that is equal to minD:
Until minD > 0, it means that we have not yet intersected any object. We can then generalize the march of the ray by:
To explain a little more progress on the radius and the complex interactions with objects, you can download SphereTracing2DApp.zip, a 2D application developed in C # that allows you to view the progress of a radius and the number of steps that must perform before falling on an intersection:
A screenshot of SphereTracing2DApp a C# 2D application to understand
SphereTracing
The white dot in the lower left is the origin of the ray (the camera). The red line is the direction of the ray. The 1st white circle is the minimum distance from the origin with all the objects in the scene (here, the blue rectangle). The ray can therefore move to that distance sphere without encountering a single object. The operation is thus repeated until an object is actually met (or minD < epsilon). The green line tells us which object has been selected from the closest "distance field".
We understand now that calculating the intersection of the camera's ray with an iso surface is in fact an incremental approximation of a bounding sphere moving towards the ray-intersection line.
Note on terminology: SphereTracing, RayMarching, DistanceFields...
As we have seen, the algorithm is to move within a distance of a sphere of radius equal to the minimum distance between the origin ray and the surface of all objects in the scene . This technique has been called Sphere Tracing by John.C.Hart. While in the demoscene, iq introduced the term distance fields, but then unfortunately eclipsed the original term which seems to me far more explicit.So when we speak of "Raymarching-Distancefields" we're actually performing a Sphere Tracing!
General algorithm Sphere Tracing
The general algorithm Sphere Tracing is the following:
ro // r0: original position of the camera
v // v: Direction of the camera
d = 0 // d: distance to the object
p = ro // p: Next position the camera
do (
d = iso (r) // Distance to object
p = p + d * v;
step++;
) while (d < epsilon && step < MAX_STEP)
If no intersection is encountered, the Sphere Tracing is stopped based on a maximum distance zfar p, or by limiting the number of steps (MAX_STEP).
Primitives
The sphere is of course not the only element we can use for modeling a surface iso. As we have seen, any function f (x, y, z) might do the trick (provided that this function returns values that do not introduce too many discontinuities on the surface). Thus, it is easy enough to use other primitives (box, cone, torus...) as described in the article by John C. Hart.Construction of a complex scene
For 4k intros, it's pretty amazing to see the complexity of scenes that can be made with this system. I have so far spoken of a single sphere. How then build more complex scenes? Using the principle CSG (Constructive Solid Geometry) as shown John.C.Hart, one of the oldest techniques in 3D modeling: it is enough to make "Boolean operations" on iso formulas: intersection, union, complement... etc..Thus, two objects, each with their respective functions iso d1 and d2, to calculate:
- The union of two objects (D1 U D2), just take a min of d1 and d2: iso (p) = min (d1 (p), d2 (p)).
- The intersection of two objects (D1 n D2), just take the max of d1 and d2: iso (p) = max (d1 (p), d2 (p)).
- The inverse of an object (-d1), simply reverse the sign iso iso (p) = -d1 (p).
- The subtraction of two objects (d1-d2) just do an intersection of d1 with the inverse of d2: iso (p) = max (d1 (p),-d2 (p))
As the scale, rotation, twist ... etc.. Example of a twist on the y-axis:
In his presentation NVScene8, iq provides a whole list of other functions: modulo, blending, noise ... etc.. Several techniques also use textures3D to apply richer transformations to iso-surfaces (see Clouds Dreams or Rudebox #main 2009).
Reflection, light, etc. ... AO.
Once we got out of the loop Sphere Tracing, if d < epsilon, p is on the surface of the object viewed. To calculate the normal to the surface, we use a gradient in p, we calculate an approximation of the derivative on the surface. Let n (p), the normal p and eps is small enough:From there, it is fairly easy to implement reflection, shadows, lighting, an OSAO (Object-Space-Ambient-Occlusion), bump mapping... this is only limited by GPU resources!
Optimizations
As we have seen, the number of steps required for a SphereTracing may be important, especially when a ray is close to an object without touching it (see the C # application to understand the phenomenon). In this case, the ray march in small steps, and the number of calculations can become very large (several times the calculation of the original iso formula of a single point). There are some way to avoid this, like using a minimum step size.For this, there are a few tips to follow:
- Minimize statements like if / then / else / switch in the code, sub-functions ... etc.. if not eliminate them.
- Therefore, avoid a scene management in the shader (if scene == 0 then this function iso, else if another function iso), but manage them outside the shader (via the compilation of different shader in GLSL, or using different pass/technique in HLSL).
- Build shaders-specific scenes (one that supports reflection, another supporting the ao + reflection) and inline initialization stage and the iso format. For this help of techniques such as "templatization" such as concatenation / substitution code to the shader initialization (which was for example used in Rudebox Alcatraz via directives #define preprocessing, or Muon baryon with a concatenation / substitution in C).
- Make a precomputation coarse stage of the scene in a texture 3D to accelerate a coarse SphereTracing, and then apply a SphereTracing on each pixel of the screen when necessary.
Next?
We have seen the principle of Sphere Tracing or RayMarching-DistanceFields, a technique widely fashionable in recent 4k intros. This technique has the advantage of being particularly simple to implement and incredibly efficient in its rendering. It's a safe bet that this technique will still be around in 2010 and that the scenes are becoming increasingly complex and rich (with, for example, the creation of specific tools to aid modeling of CSG scenes).Code sample : SphereTracing2DApp.zip is a C# 2D application showing the ray marching algorithm in action.
This article was initially written for the www.demoscene.fr web site. It's an imperfect translation quickly done with google translator service and with few minor changes. Tell me if there is anything wrongly explained here! ;)